Three Square Problem
Three squares are placed in a row Connect the bottom left corner of each square to The top right corner of the third square These form three angles with the horizontal a,b,c
What is a + b + c is equal to
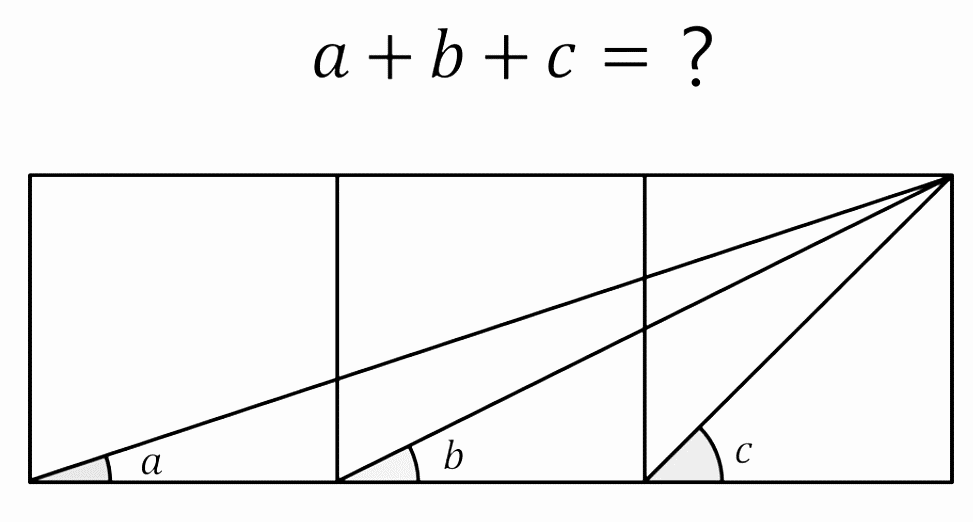
show that a + b + c = 90
Solution
using trigonometry and inverse trigonometry
Let the side of the square be one unit, then
c
{\color{DarkBlue} tan\;c=\frac{1}{1} } \\ {\color{DarkBlue} c=45\degree }b
{ \color {DarkBlue} tan\;b = \frac{1}{2} } \\ \\ \\ {\color {DarkBlue} b = tan^{-1}\frac{1}{2} }a
{ \color {DarkBlue} tan \; a = \frac{1} {3} } \\ \\ \\ {\color {DarkBlue} a = tan^{-1}\frac{1}{3} }a+b+c=tan^{-1}\frac{1}{3}+tan^{-1}\frac{1}{2}+45\degreeby using Inverse Trigonometric Function
{ \color{Red} tan ^ { -1 } a + tan ^ { -1 } b = tan ^{ - 1} \frac{a+b}{1-ab}, \; if \;the \; value \; xy < 1}tan^{-1}\frac{1}{3} + tan^ {- 1} \frac { 1 } {2} = tan^ {-1} \frac { \frac {1} {3}+ \frac {1} {2} } { 1 - \frac {1} {3} \frac {1 } {2}} \\ tan^ {-1} \frac{ \frac{2+3} {6}} { \frac {6-1} {6} }= tan ^ { -1 } \frac { \frac {5} {6} } { \frac {5} {6} }=tan^ {-1} 1 = 45 \degree {\color{Teal} a + b = 45 \degree} \; and \; {\color{Teal} c=45 \degree}Sum of three angles is
{ \color {Teal} a + b + c = 90 \degree} hard math problems for 10th graders
hard math word problems with answers
hard geometry problems with answers
easy math problems that look hard
easy geometry problems that look hard